テクノロジー
2024年11月15日ロジスティック回帰とは

ロジスティック回帰(Logistic regression)とは、ベルヌーイ分布・二項分布に従う分類モデルで一般線形モデルの一種です。
著者プロフィール
IT分野における教育の先駆者として、多くのエンジニアを育成するプログラミングスクールの運営、Web開発やAI研修を行なっています。幅広いレベルの受講生に対して実践的なスキルを提供。生徒の成長を第一に考え、効果的で魅力的な教育プログラムの設計に情熱を注いでいます。
ゴール
- 「機械学習スクラッチ ロジスティック回帰」を解くうえで必要な知識について理解する
目的
- ロジスティック回帰を理解する
- ロジスティック回帰をスクラッチ開発するのに必要な概念を理解する
ロジスティック回帰
ロジスティック回帰とは
主に生存分析(生きるか死ぬか)などで用いられるアルゴリズムです。
生存分析は、病気や医療の領域だけでなく広義には、ユーザーが特定の行動を起こすか否かというような問題にも適用され、様々な領域・分野で用いられます。
つまり、簡単に言うと、ある事象が起こる確率を算出するアルゴリズムです。
数学的な側面の説明
ロジスティック回帰(Logistic regression)とは、ベルヌーイ分布・二項分布に従う分類モデルで一般線形モデルの一種です。
まず、一般線形モデルは線形回帰のように変数に対して任意の係数をかけたものを足した値を、変数の線型結合と言います。
この線形結合した値を「関数で変換」して最終的な予測結果を得るものです。
ロジスティック回帰の出力は、「ある事象が起こる確率」であり、この出力結果からクラスの分類を行います。
具体的には、線形回帰の出力をあとで紹介するシグモイド関数に通したものがロジスティック回帰の出力となります。
上記の方法で確率を回帰していることから「回帰」と名付けられています。
従って、ロジスティック回帰も一方の変数を他方の変数(要因ごとに重みをかけた上で)によって説明しようとする点は線形回帰と変わりません。
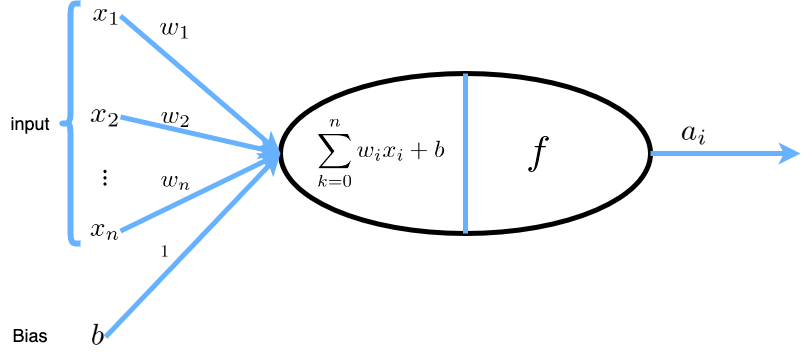
ロジスティック回帰のイメージ
ロジスティック回帰は、 隠れ層のないニューラルネットワークと同じ構造であることから、ロジスティック回帰の理解は、深層学習への橋渡しとなります。
ロジスティック回帰の前提
- 説明変数(x)は連続値 or 離散値で、目的変数(y)は離散値。
- ロジスティック回帰の出力値は0〜1の連続値
- 最終的な予測値は、0または1ベルヌーイ分布・二項分布(平均np、分散np(1-p))に従う
まとめ
- ロジスティック回帰はクラス分類をするときに使われる
- ロジスティック回帰はニューラルネットワークと密接な繋がりがある